Are you looking for an answer to the topic “Control system – Solved examples of Mason’s Gain Formula“? We answer all your questions at the website Chambazone.com in category: 40+ Marketing Blog Topics & Ideas. You will find the answer right below.
Keep Reading
Table of Contents
Mason’s Gain Rule (Solved Example 1)
Images related to the topicMason’s Gain Rule (Solved Example 1)
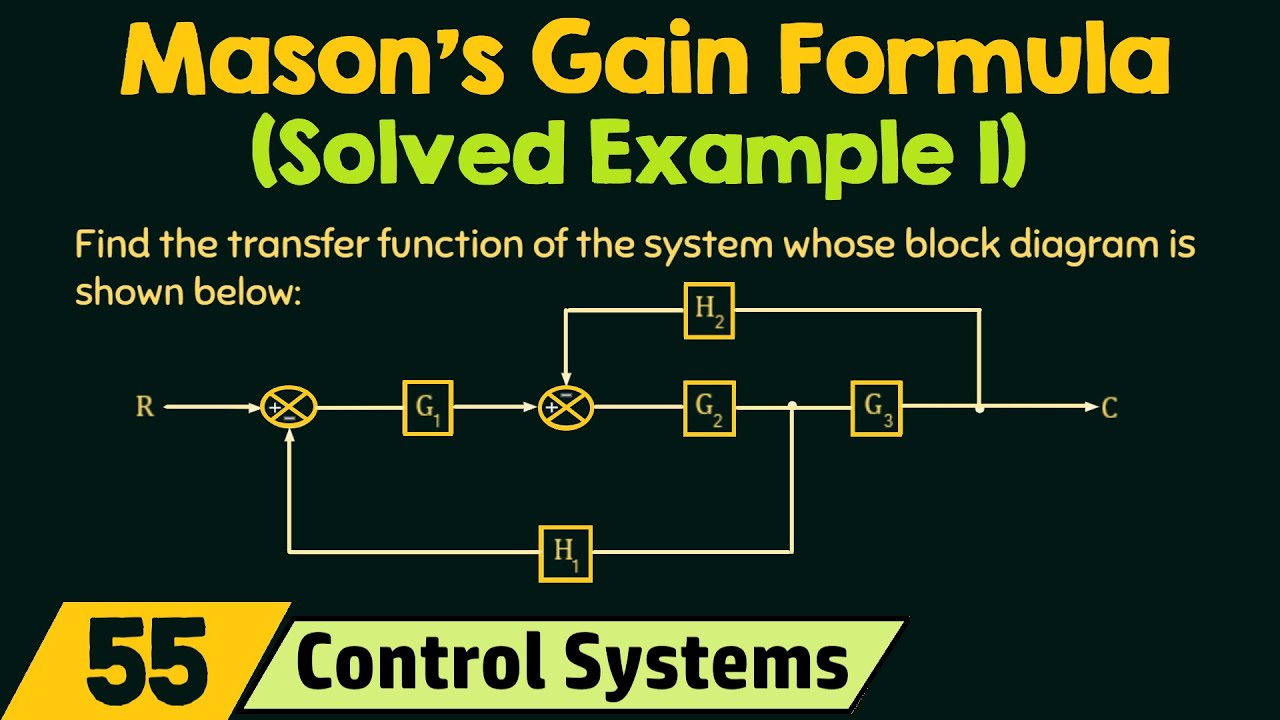
We all know that practice is really the key to success, so you should practice these concepts heavily from well-known books to refresh your solving skills. In this post, we will continue our previous post concept, which is H. “Mason Gain Formula” (Applied section). Before we start, I hope you have understood all the terms we will use extensively here to solve problems (from my previous post). So let’s move on. We have mainly three different types of questions (on this topic), viz. H.: The application of the Mersenne gain formula when: Given a block diagram (or signal flow graph), we need to find the overall transfer function. Solve the signal flow graph for the given equation. The gr is given. So let’s look at these three parts in turn. We already know how to derive a signal flow diagram from any block diagram model. Let’s see how Mason’s gain equation works now: Here we want to obtain the transfer function for the following signal flow graph. Now we have to follow the steps described in my previous post, Step 1: Get the forward path From the flowchart, we can notice that there are two forward paths in total i.e. H. Step 2: Total Loop. Now that we’ve found the required forward path, we need the total number of loops. If you look closely, there are a total of 5 loops in the signal flow graph. = , = , , = , = , , = , Step 3: Total 2 cycles without contact: = = Step 4: No 3 cycles without contact. Step 5: Value of Δ Δ = 1 – + therefore Δ = 1 – Step 6: Find the value of and : All loops touch the forward path. So the = 1 loop doesn’t touch the forward path. So = 1 – = (1 -) Now, using Mason’s gain formula, the total transfer function can be given: TF = C/R = You can refer to the diagram below to see what the 5 loops we used have struggled to figure out. This concludes our first variant i. H. Derive the transfer function from the given signal flow graph. Now we move on to the second and third varieties. (Both can be sa to be a subset of the first variant, since for both we need to export the signal flow graph first, and then we have to follow the normal steps we follow for the first variant). Given a block diagram, we first have to derive the signal flow graph as shown below: Step 1: Get forward paths: There are two forward paths = 1 and 2 = Step 2: Get total number of single loops: = – Step 3: Get the count of two loops that don’t touch each other: There are no two loops that don’t touch each other. Step 4: Find the value of Δ: Δ = 1 – = 1 – Step 5: Find the value of the sum due to the loop touching and . So, = 1 , = 1 Step 6: Using Mason’s gain formula, we have: TF = C(s)/R(s) = TF = Now let’s look at the last number in this topic: Suppose, give Define the equation as; ; ; has four nodes, and . We will now graph the signal flow using the above equation: Step 1: Find the number of forward paths: Step 2: Find the total number of loops; ; Step 3: Determine the number of non-contact loops. There are no two contactless cycles. Step 4: Find the value of Δ: Δ = 1 – ; Δ = 1 – ; Step 5: Find the value: = 1 since both loops touch all four forward paths Step 6: Use Mason’s gain formula, we get the transfer function: Finally, we reach the end of this post. I’ll share more resolved examples in PDF format later in this post. I ask you to check the problem first (not the solution) and after you try it, check the solution given at the end of the documentation. Stay tuned for the next important (and interesting) topic of this thread in my next post. report this ad
What is Mason’s gain formula in control system?
Mason’s gain formula (MGF) is a method for finding the transfer function of a linear signal-flow graph (SFG). The formula was derived by Samuel Jefferson Mason, whom it is also named after.
What is Mason’s gain formula explain with the help of example?
It is a technique used for finding the transfer function of a control system. Basically, a formula that determines the transfer function of a linear system by making use of the signal flow graph is known as Mason’s Gain Formula. It shows its significance in determining the relationship between input and output.
What is the forward path gain?
Forward path gain: A product of all branches gain along the forward path is called Forward path gain. Loop Gain: Loop gain is the product of branch gain which travels in the loop.
What is order and type of the system explain with example?
The Order is defined as maximum power of S in denominator. The Type is defined by value of n in denominator, ie. no of poles at origin only. Both Order and Type of system are independent to number of zeros of transfer function. Example 1: G(S)= K/S(S+1) it is of 2nd order type 1 system.
How do you solve a block diagram in a control system?
Rule 1 − Check for the blocks connected in series and simplify. Rule 2 − Check for the blocks connected in parallel and simplify. Rule 3 − Check for the blocks connected in feedback loop and simplify. Rule 4 − If there is difficulty with take-off point while simplifying, shift it towards right.
Which of the following is an example of open loop control system?
The open-loop control system can be described by a block diagram as shown in the figure below. These are the systems in which the control action is independent of output. Example: Traffic signals, bread toaster, sprinkler, ordinary washing machine, and systems having no sensor, etc.
How do you find the steady state error in a control system?
…
Example.
| Input signal | Error constant | Steady state error |
|---|---|---|
| r2(t)=2tu(t) | Kv=lims→0sG(s)=∞ | ess2=2Kv=0 |
| r3(t)=t22u(t) | Ka=lims→0s2G(s)=1 | ess3=1ka=1 |
See some more details on the topic Control system – Solved examples of Mason’s Gain Formula here:
Mason’s Gain Formula – Tutorialspoint
Examples − y1→y2→y3→y4→y5→y6 and y1→y2→y3→y5→y6. Forward Path Gain. It is obtained by calculating the product of all branch gains of the forward path.
Control system – Solved examples of Mason’s Gain Formula
In this post you will find all the varieties of different kind of numericals from Mason’s Gain Formula . Also you can see some good Mason Gain examples.
Mason’s Gain Formula – Explanation with Examples
A method that determines the transfer function of a linear system by making use of the signal flow graph is known as Mason’s Gain Formula.
Control System Mason Gain Formula – Javatpoint
The relation between an input variable and an output variable of a signal flow graph is given by Mason’s Gain Formula. … Where,. Pk = forward path gain of the K …
Related searches to Control system – Solved examples of Mason’s Gain Formula
- masons gain formula pdf
- masons rule block diagram
- mason’s gain formula pdf
- mason gain formula to determine transfer function
- mason formula
- Mason formula
- Signal flow graph
- sfg examples
- control system graph
- mason’s rule block diagram
- mason gain formula solved examples pdf
- signal flow graph
Information related to the topic Control system – Solved examples of Mason’s Gain Formula
Here are the search results of the thread Control system – Solved examples of Mason’s Gain Formula from Bing. You can read more if you want.
You have just come across an article on the topic Control system – Solved examples of Mason’s Gain Formula. If you found this article useful, please share it. Thank you very much.
