Are you looking for an answer to the topic “Area Of Triangle Formula For All Types Of Triangle – Detailed Steps !!“? We answer all your questions at the website Chambazone.com in category: 40+ Marketing Blog Topics & Ideas. You will find the answer right below.
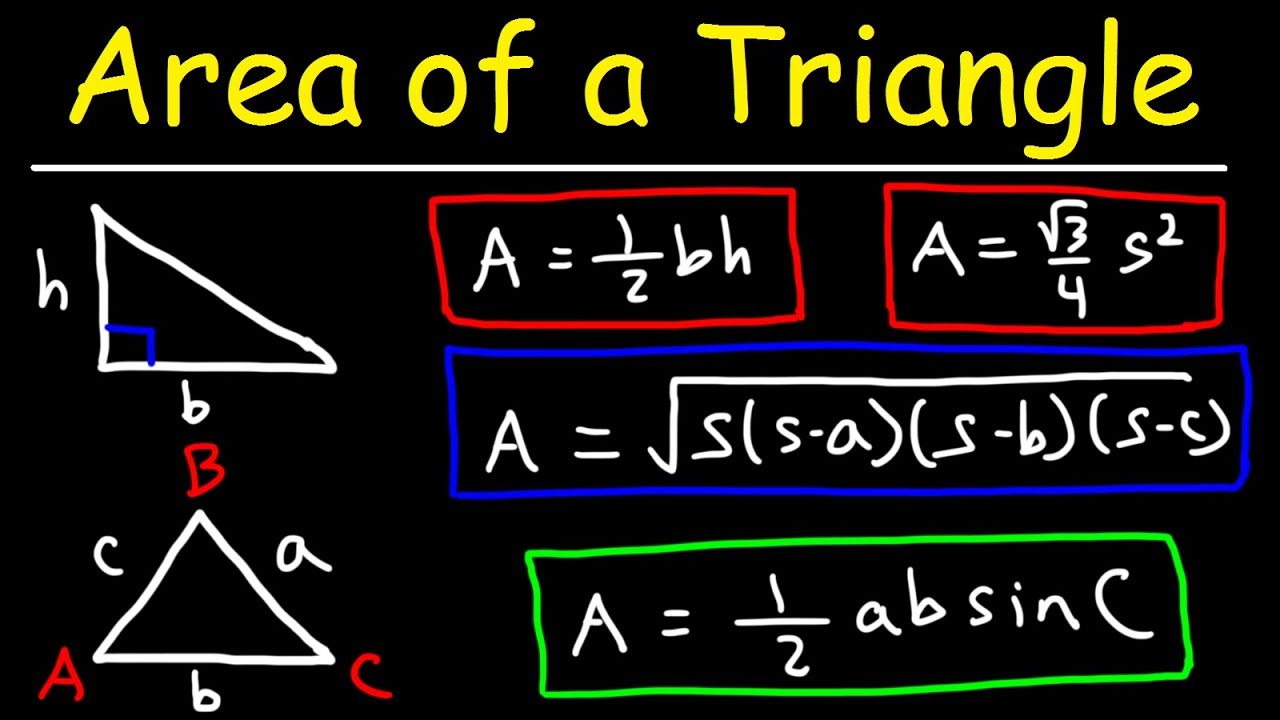
The basic formula for the area of a triangle is equal to half the product of its base and height, i.e., A = 1/2 × b × h. This formula is applicable to all types of triangles, whether it is a scalene triangle, an isosceles triangle, or an equilateral triangle.The area of a triangle is defined as the total region that is enclosed by the three sides of any particular triangle. Basically, it is equal to half of the base times height, i.e. A = 1/2 × b × h.What is the Area of a Triangle with three Sides and an Angle? If the sides of a triangle are given along with an included angle, the area of the triangle can be calculated with the formula, Area = (ab × sin C)/2, where ‘a’ and ‘b’ are the two given sides and C is the included angle.
| Based on their Sides | Based on their Angles |
|---|---|
| Scalene Triangle | Acute Triangle |
| Isosceles Triangle | Obtuse Triangle |
| Equilateral Triangle | Right Triangle |
Table of Contents
Area of a Triangle, Given 3 Sides, Heron’s Formula
Images related to the topicArea of a Triangle, Given 3 Sides, Heron’s Formula
In this article, we will see different types of triangle area formulas. We will see many types of cases through which you will illustrate concepts related to all types of triangles. After learning all the concepts, you will be able to solve many problems. These will be very easy to understand. So let’s get started.
How To Find Area Of Triangle ?
asks for the area of a triangle, and we need to follow different formulas depending on different situations explained below: In a right triangle, the area is simply given by knowing the base and height of the triangle. In a scaled triangle, for the region where we need all ses of the triangle, then we can apply Heron’s formula. Given two ses and the angle between the two ses, then we can also use trigonometric functions to find the area. For equilateral and isosceles triangles, we can give the area directly if we know the se measurements. If we have the coordinates of all the vertices, we can use coordinate geometry to find the area of a triangle. For all the above cases, now let’s look at different formulas to find the area of a triangle along with examples for better understanding.
Type 1 : Area Of A Right Triangle Formula !!
This is the easiest way to find the area in any right triangle using the formula below. To do this, we need to explicitly know the base and height of the triangle. Even if one of the edges is not given, we have to use the famous Pythagorean formula to find the desired edge: We all know that the Pythagorean formula is: (hypotenuse)² = (height)² + (base )² Case 1: Right triangle with known ses! ! When you get an acute right triangle, two ses are proved, the height and the base. Then you can easily calculate the area. The area of a triangle is given by: Area formula: 1/2 × base × height = (base × height)/2 Case 2: Area of an obtuse triangle! ! When you get a triangle with an angle greater than 90°. Again, you get the height and base, but for this type of triangle we need to construct a height. Just extrapolate the base and connect a line from a point. Then just apply the same formula as above. The formula for the area of a triangle: 1/2×base×height=(base×height)/2 Now we can see in the figure below that the vertical line drawn down from the point “C” intersects the extension line, drawn from the point “C” A” ‘ . So we get the height, with base AB (a unit). The same formula for area can be used for the area of an isosceles triangle, as shown in the next section.
Type 2 : Area Of An Isosceles Triangle Formula !!
In an isosceles triangle, always remember that the two ses (and angles) are equal. So to find the area, we need to find the base and height exactly. So now if you have an isosceles triangle where two ses are equal and assume all ses are given. Again, you need to draw the elevation (vertical line from C ) by splitting to the right of the center of the base. In the image above, the measure of “b” = AB/2, so the base bisects. Now you can use the Pythagorean theorem to find the height, which is the formula: Pythagorean formula: – a² + b² = c² (the value of ‘a’ can be obtained from this) Triangle area: – 1/2 × base × height.
Type 3 : Area Of An Equilateral Triangle !!
Suppose you get an equilateral triangle. In this triangle, we make all three ses equal. Also, the angles are equal and 60°. Method 1: Find the area of this triangle, the method is the same as above. We first use the Pythagorean theorem to find the height by drawing a line perpendicular to the base. Formula: Pythagorean Theorem: – a² +b² = c² where b = AB/2 = c/2 (AB = BC = CA = ‘c’) Now the area can be given as: Triangle area: – × 1.1 base × height method 2: If you get an equilateral triangle, there is an easier way to find the area. You need to use the formula and calculate it. The formula for the area of an equilateral triangle: √3/4 × (se)² Here, the se is the measure of the se of the equilateral triangle. (AB = BC = CA and ∠A = ∠B = ∠C = 60°).
How To Find Area Of Triangle With Two Ses Given And Using Trigonometry !!
Here you get a triangle, two ses, and an angle, in the following order: se-angle-se (SAS). Let’s make the angles A,B,C and the ses a,b,c. Here the ses a and b are given, and the angle C (between ses a and b) is given. The formula for the area of a triangle: 1/2×a×b×Sin C.
How To Find Area Of Triangle With All Three Ses Given !!
Now if you get a triangle (SSS) with three given ses. Here, you need to use Heron’s formula. A triangle has three ses a,b,c. and be given. Here the first thing to do is to find the half perimeter ‘s’ = (a+b+c)/2; the perimeter of any triangle is simply given by: a + b + c (where a, b and c are the ses of the triangle) and finally Area of triangle without height given by Heron’s formula = So if only ses are given we can also find the area by simply using Heron’s formula.
How To Find Area Of Triangle Without Height Given ?
Now this is interesting. What if we don’t have height. As you can see above, finding the area of a triangle is fairly easy once you know the height and base of the triangle. But if we don’t have the height, it’s easy to find the area too. In this case, we have to use Heron’s formula (when all ses i.e. SSS are known) and also given two ses and an included angle (SAS), we can directly use the trigonometry shown above. For example, if the ses of a triangle are specified as 8 cm and 4 cm, respectively. Also, the included angle is 30°. Then find the area of the given triangle. Here, we should now find the area of the triangle without height. So we have two adjacent ses and an included angle. So the formula for a triangle is: Area ΔABC = 1/2 * AB * BC * sinB We know that sinB = sin30° = 1/2 = 0.5 so the area is = 1/2 * 4 * 8 * 0.5 = 8 cm² Now, given With all three ses and no height, we can quickly use Heron’s formula. If the three ses of the triangle are 4 cm, 7 cm and 5 cm respectively. Then find the area of the given triangle. Here, we should now find the area of the triangle without height. So we have all three ses (SSS), so Heron’s formula can be easily used by first finding half the perimeter. Therefore, the formula for a triangle is: Half perimeter = ‘s’ = (AB + BC + AC)/2 = (4+5+7)/2 = 8 units of area Using the series formula = where, AB = a , BC = b , AC = c , now set the boundary values as above: area ΔABC = 9.79 cm².
How To Find Area Of Triangle Using Coordinate Geometry !!
In cogo, if we know the x- and y-coordinates of all three vertices, we can use their area formulas directly. Suppose we have three vertices A(x1,y1), B(x2,y2) and C(x3,y3). Now we have the formula for the area of the triangle as: Triangle area: (1/2)[x1(y2 – y3) + x2(y3 – y1) + x3(y1 – y2)] sq units Now we can even separately by using the distance formula Find the length of each se to apply Heron’s formula, then apply Heron’s formula. Now the calculation becomes easier when you see that one of the vertices above is the origin, and in this case we also have an area formula: the area of the triangle when one vertex is the origin: (x2*y3 – x3* y2)/ 2 We use vertex A as the origin to calculate the above formula. If desired, you can manually enter the value of point A(x1,y1) as (0,0). I hope you really enjoyed this post on methods to find the area of a triangle. Let me know if you have any questions about this. Stay tuned for more interesting content in this series. report this ad
What is the area formula for all triangles?
The area of a triangle is defined as the total region that is enclosed by the three sides of any particular triangle. Basically, it is equal to half of the base times height, i.e. A = 1/2 × b × h.
How do you find the area of a triangle with all three sides?
What is the Area of a Triangle with three Sides and an Angle? If the sides of a triangle are given along with an included angle, the area of the triangle can be calculated with the formula, Area = (ab × sin C)/2, where ‘a’ and ‘b’ are the two given sides and C is the included angle.
What are the 9 types of triangle?
| Based on their Sides | Based on their Angles |
|---|---|
| Scalene Triangle | Acute Triangle |
| Isosceles Triangle | Obtuse Triangle |
| Equilateral Triangle | Right Triangle |
Does Heron’s formula work for all triangles?
The above area of triangle formula is applicable for all triangles irrespective of the side lengths.
How do you find the area with different sides?
- Area = side × side or A = s. …
- Example: If one side of a square has a length of 4 feet, (t = 4), then the area of this square is simply t2, or 4 x 4 = 16 square feet.
What are the 12 types of triangles?
- Scalene Triangle. A triangle that has no congruent sides.
- Acute Triangle. A triangle that has all three angles with measures of less than 90 degrees.
- Obtuse Triangle. A triangle that has one angle with a measure of greater than 90 degrees.
- Isosceles Triangle. …
- Equilateral Triangle. …
- Right Triangle.
What is triangle and its formula?
The basic formula for the area of a triangle is equal to half the product of its base and height, i.e., A = 1/2 × b × h. This formula is applicable to all types of triangles, whether it is a scalene triangle, an isosceles triangle, or an equilateral triangle.
What are the 7 types of triangles?
To learn about and construct the seven types of triangles that exist in the world: equilateral, right isosceles, obtuse isosceles, acute isosceles, right scalene, obtuse scalene, and acute scalene.
See some more details on the topic Area Of Triangle Formula For All Types Of Triangle – Detailed Steps !! here:
Triangles: Area – Varsity Tutors
The area of each triangle is one-half the area of the rectangle. So, the area A of a triangle is given by the formula A=12bh where b is the base and h is …
Area of a Triangle: Learn Formulas and Methods to Calculate …
The first step is to determine the semi perimeter of a triangle by summing all the three ses of a triangle and diving it by two. The next …
Area Of Triangle Formula For All Types Of Triangle
Here you can get all the formula for finding the area of triangle quickly .Also you can find the area of equilateral , scalen and isosceles …
Properties of Triangle – types & formulas [Video & Practice]
The sum of all internal angles of a triangle is always equal to 180°. … Let’s look into the six types of triangles in detail:.
Related searches to Area Of Triangle Formula For All Types Of Triangle – Detailed Steps !!
- area of the triangle with vertices
- Area of triangle
- calculate area of triangle given 3 points
- Area of equilateral triangle
- area of trapezium
- Area of trapezium
- area of triangle
- area of a rectangle
- area of equilateral triangle
- Area of a rectangle
- Area of parallelogram
- area of parallelogram
- Area of the triangle with vertices
- area of circle
Information related to the topic Area Of Triangle Formula For All Types Of Triangle – Detailed Steps !!
Here are the search results of the thread Area Of Triangle Formula For All Types Of Triangle – Detailed Steps !! from Bing. You can read more if you want.
You have just come across an article on the topic Area Of Triangle Formula For All Types Of Triangle – Detailed Steps !!. If you found this article useful, please share it. Thank you very much.
