Are you looking for an answer to the topic “Basics of Elliptical Curve Cryptography !! (The Ultimate Guide)“? We answer all your questions at the website Chambazone.com in category: 40+ Marketing Blog Topics & Ideas. You will find the answer right below.
Keep Reading
Elliptic Curve Cryptography Overview
Images related to the topicElliptic Curve Cryptography Overview
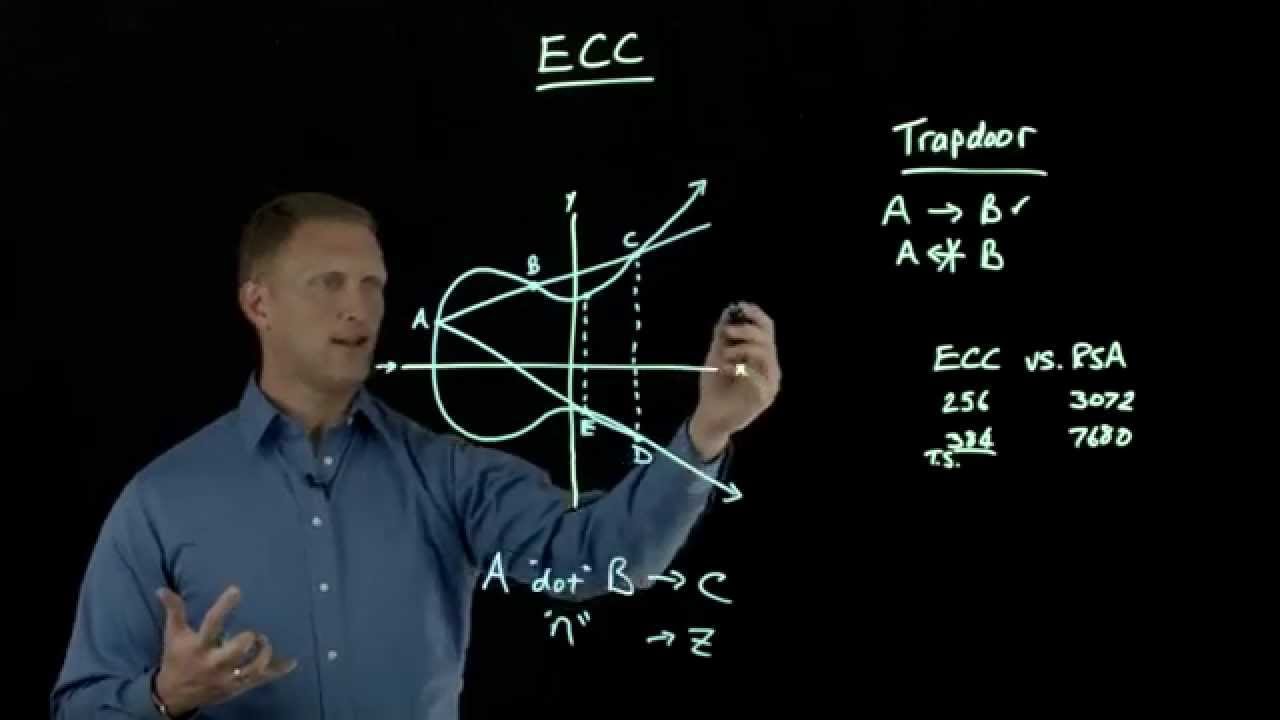
So far, we have seen key-based encryption and decryption modes in symmetric and asymmetric types of cryptographic processes. Now Elliptic Curve Cryptography is actually an improved and more efficient (faster, more secure) way of cryptography. We’ll be covering ECC in detail here, so sit back and read on. Elliptic Curve Cryptography (ECC) was developed as an alternative to traditional public key cryptosystems such as Rivest Shamir Adelman, Digital Signature Algorithms, and Diffie Hellman. Elliptic curve cryptography proves equivalent security with a smaller key size, ie. H. 160 bits, while RSA uses 1024 bits. ECC can speed up computation, reduce power consumption, and save disk space and bandwth usage. ECC was developed by Neal Koblitz and Victor S. Miller in 1985 using elliptic curves in cryptography.
What Is Elliptic Curve Cryptography (ECC) ?
Elliptic Curve Cryptography (ECC) is a public key cryptography method based on the algebraic structure of elliptic curves over finite fields. Since 1985, ECC has been under intense scrutiny by cryptographers, mathematicians and computer scientists around the world. ECC found no obvious weaknesses, and there is a high level of confence in the security of ECC. ECC is becoming more powerful and attractive than RSA and DSA. Top standards bodies such as ANSI, IEEE, and ISO have proven that ECC has grown in popularity in recent years. An elliptic curve is a solution set of equations of the form: y^2 = x^3 + ax + b where the coefficients a and b are the elements of the field. Each value of “a” and “b” gives a different elliptic curve. Such equations can be explored through various mathematical structures such as rings or finite fields. An interesting property of elliptic curves is that they form a group that allows us to do cryptography. The public key is a point on the curve, and the private key is a random number, as shown in the figure below. The public key is obtained by multiplying the private key by the generation point G on the curve.
Elliptic Curve Cryptography Encryption And Decryption Process !!
There are various methods for ECC encryption and decryption. The following method is one of them. The first task of the system is to encode the plaintext message “m” to be sent as an x-y point Pm. The point Pm is encrypted as ciphertext and then decrypted. Note that we cannot simply encode the message as the x or y coordinates of a point, because not all of these coordinates are in Ep(a,b) . where Ep(a,b) are the coordinates of the group element representing the message. Ep(a,b) represents the elliptic group mod p whose elements (x,y) are pairs of non-negative integers less than p that satisfy the following equation; y^2 = x^3 + ax + b (mod p) where a and b are non-negative integers less than p that satisfy the following equation: 4a^3 + 27b^2 . (mod p) 9 ≠ 0 The encryption/decryption system requires a point G and an elliptic group Ep(a,b) as parameters. Each user A chooses a private key Ar and generates a public key Pu = Ar xG. To encrypt a message Pm and send it to B, A chooses a random positive integer x and generates a ciphertext Cf consisting of point pairs Cf = {xG, Pm + xPb}. Here, A uses B’s public key Pb. To decrypt the ciphertext, B multiplies the first point of the key pair by B’s key and subtracts the result from the second point: Pm + xPb – Br(xG) = Pm + x(BrG) – Br( xG) = Pm A has masked the message Pm by adding xPb. Only A knows the value of x, so no one can remove the mask xPb even if Pb is the public key. However, A also contains a “hint” sufficient to remove the mask, knowing the private key Br. In order for the attacker to recover the message, the attacker needs to compute X given G and xG, which is difficult. I hope you really enjoyed this article on elliptic curve cryptography. Stay tuned for more interesting content in this series.
See some more details on the topic Basics of Elliptical Curve Cryptography !! (The Ultimate Guide) here:
Basics of Elliptical Curve Cryptography !! (The Ultimate Guide)
The Elliptic curve cryptography (ECC) is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite …
Guide to Elliptic Curve Cryptography – SpringerLink
Anchored by a comprehensive treatment of the practical aspects of elliptic curve cryptography, this gue explains the basic mathematics, …
Guide to Elliptic Curve Cryptography – CiteSeerX
Gue to elliptic curve cryptography / Darrel Hankerson, Alfred J. Menezes, Scott Vanstone. p. cm. Includes bibliographical references and index.
Guide to Elliptic Curve Cryptography (Springer Professional …
Anchored by a comprehensive treatment of the practical aspects of elliptic curve cryptography (ECC), this gue explains the basic mathematics, …
Related searches to Basics of Elliptical Curve Cryptography !! (The Ultimate Guide)
- basics of elliptical curve cryptography the ultimate guide examp
- basics of elliptical curve cryptography the ultimate guide exampli
- elliptic curve cryptography pdf
- basics of elliptical curve cryptography the ultimate guide holid
- basics of elliptical curve cryptography the ultimate guide htt
Information related to the topic Basics of Elliptical Curve Cryptography !! (The Ultimate Guide)
Here are the search results of the thread Basics of Elliptical Curve Cryptography !! (The Ultimate Guide) from Bing. You can read more if you want.
You have just come across an article on the topic Basics of Elliptical Curve Cryptography !! (The Ultimate Guide). If you found this article useful, please share it. Thank you very much.
