Are you looking for an answer to the topic “Equation Of A Circle In It’s Standard Form & Some Examples With Steps !!“? We answer all your questions at the website Chambazone.com in category: 40+ Marketing Blog Topics & Ideas. You will find the answer right below.
The graph of a circle is completely determined by its center and radius. Standard form for the equation of a circle is (x−h)2+(y−k)2=r2. The center is (h,k) and the radius measures r units.
Table of Contents
Graph the equation of a circle from its standard form
Images related to the topicGraph the equation of a circle from its standard form
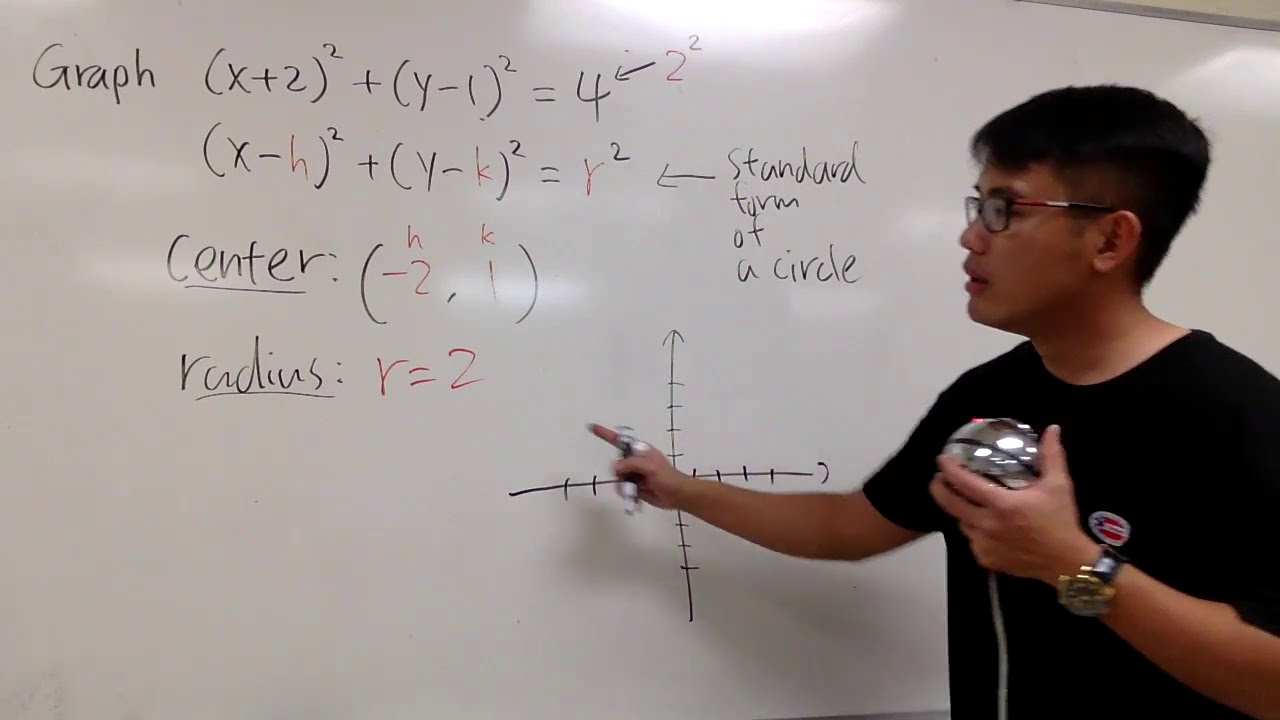
The circle is indeed one of the basic geometric figures that we encounter in our daily life. In this post, we’ll explore the finer details as well as the standard equations for circles. Also, we will see some common examples related to the circle equation. So first we need to understand what the equation of a circle looks like. In each circle, we only need a center point and a radius as the only parameters to fully define it. What is the general equation for a circle? First, let’s briefly understand the general equation of a circle. Therefore, the standard equation for a circle with center (h,k) and radius “a” is: Circle equation: (x – h)² + (y – k)² = a² to be written as x² + y² + 2gx + 2fy + The shape of c = 0 is given; in the above equation we have any three constants, H. g , f and c , have two variables at the same time, namely H. x and y. In the general equation above, the center of the circle is (-g , -f) and the radius of the circle is . The above equation will become clearer as you continue reading this article. You will receive all the details of this circle equation along with example exercises.
What Is Circle In Exact Mathematical Terms ?
The mathematical definition of a circle is a geometric figure representing the trajectory of a point moving on a plane such that its distance from a fixed point on that plane is always a constant value. Now the fixed point is called the center of the circle and the constant distance is called the radius of the circle. The circle equation basically refers to the generalized equation of the circumference that gives the relationship between the coordinates of the moving point P(x,y), including some constants that depend on the position of the center of the circle and the length of the radius of the circle. In simple terms, we can say that a circle equation is almost the set of all points lying on the circumference of the circle. So the standard equation for a circle with center (h,k) and radius ‘a’ is: Circle equation: CP² = a²; .. (Applying the distance formula, the distance between two points, i.e. C(h,k ) and P(x,y) and square both ses) (x – h)² + (y – k)² = a² ; Now let’s look at some general and special case circle equations. So, in the next section, we’ll take a deeper look at the equations of circles.
How To Find The Equation Of Any Circle Whose Center And Radius Are Given ?
Let ‘O’ be the center of the circle and coordinates be (h,k) . Now let’s assume point P(x,y) be any random point moving on the circumference of the circle. Now from coordinate geometry, we already know that the distance between two coordinates is given by : Distance OP = Now this distance will be the radius of the circle, let say the radius is a constant ‘a’ . Now applying the distance formula (squaring both se), we will get the following generalized standard equation of a circle : (x – h)² + (y – k)² = a² ; Now let’s see some special cases of this equation and also derive the equation of the circle in each case : Case 1. Circle equation with center at origin (0,0) If the center is at origin i.e. O(0,0) . Then putting values of (h,k) as (0,0) in the above standard equation of circle , we’ll get the equation of the circle : x² + y² = a² Case 2. When the circle passes through the origin Let us understand this case using proper diagrams as below : In the right triangle OCM , we can apply the Pythagoras theorem as below : OC² = OM² + CM² i.e. a² = h² + k² …………. (1) We already know the standard equation of the circle as i.e. (x – h)² + (y – k)² = a² ; Now from equ (1) , putting the value of the term ‘a²’ in the above equation : (x – h)² + (y – k)² = h² + k² ; On simplifying the above , the circle equation is given as = x² + y² – 2hx – 2ky = 0 Thus , if the circle passes through the origin (0,0) , then we have the equation of the circle as given above. Case 3. When the circle touches the x-axis Let us understand this case using proper diagrams as below : If (h,k) is the center of the circle and if the circle touches the x-axis , then : Clearly, a = k (i.e. the radius of the circle) ……equation (1) We already know the standard equation of the circle as i.e. (x – h)² + (y – k)² = a² ; Now from equ (1) , putting the value of the term ‘a²’ in the above equation : (x – h)² + (y – k)² = k² ; On simplifying the above , the circle equation is given as = x² + y² – 2hx – 2ay + h² = 0 Thus , if the circle touches the x-axis, then we have the equation of the circle as given above. Case 4. When the circle touches the y-axis Let us understand this case using proper diagrams as below : If (h,k) is the center of the circle and if the circle touches the y-axis , then : Clearly, a = h (i.e. the radius of the circle) ……equation (1) We already know the standard equation of the circle as i.e. (x – h)² + (y – k)² = a² ; Now from equ (1) , putting the value of the term ‘a²’ in the above equation : (x – h)² + (y – k)² = h² ; On simplifying the above , the circle equation is given as = x² + y² – 2ax – 2ky + k² = 0 Thus , if the circle touches the y-axis, then we have the equation of the circle as given above. Case 5. When the circle touches both the axes Let us understand this case using proper diagrams as below : If (h,k) is the center of the circle and if the circle touches both x-axis and y-axis , then : Clearly, h = a = k (i.e. the radius of the circle) ……equation (1) We already know the standard equation of the circle as i.e. (x – h)² + (y – k)² = a² ; Now from equ (1) , putting the value of the term ‘a²’ in the above equation : (x – a)² + (y – a)² = a² ; On simplifying the above , the circle equation is given as = x² + y² – 2ax – 2ay + a² = 0 Thus , if the circle touches both the axes, then we have the equation of the circle as given above. Case 6. When the circle passes through the origin and Center lies on the x-axis Let us understand this case using proper diagrams as below : If (h,k) is the center of the circle and if the circle passes through the origin and center lies on x-axis, then : Clearly, k = 0 and h = a (i.e. as the centre lies on x-axis , y value will be ‘0’) …….equation (1) We already know the standard equation of the circle as i.e. (x – h)² + (y – k)² = a² ; Now from equ (1) , putting the value of the term ‘a²’ in the above equation : (x – a)² + (y – 0)² = a² ; On simplifying the above , the circle equation is given as = x² + y² – 2ax = 0 Thus , circle passes through the origin (0,0) and center lies on the x-axis, then we have the equation of the circle as given above. Case 7. When the circle passes through the origin and Center lies on y-axis Let us understand this case using proper diagrams as below : If (h,k) is the center of the circle and if the circle passes through the origin and center lies on the y-axis , then : Clearly, k = a and h = 0 (i.e. as the center lies on y-axis , x value will be ‘0’) …….equation (1) We already know the standard equation of the circle as i.e. (x – h)² + (y – k)² = a² ; Now from equ (1) , putting the value of the term ‘a²’ , h and k in the above equation : (x – 0)² + (y – a)² = a² ; On simplifying the above , the circle equation is given as = x² + y² – 2ay = 0 Thus, circle passes through the origin (0,0) and center lies on the y-axis, then we have the equation of the circle as given above. .
What Is The General Equation Of A Circle And Its Applications ?
As shown above, the general equation for a circle is x² + y² + 2gx + 2fy + c = 0 ; in the above equation, we have any three constants, which are H. g , f and c , have two variables at the same time, namely H. x and y. In the general equation above, the center of the circle is given as (-g , -f) and the radius of the circle is now problematic, to use this general form of circle we need some simple formulas. That is, you can quickly predict the center and radius of a circle by simply consering any complex quadratic polynomial. So if you get an equation of the form: x² + y² + 2gx + 2fy + c = 0 ; then simply the center of the circle = (-g , -f) = [-(coefficient of x)/2 , -(coefficient of y)/2] the circle radius becomes = = now set the value of g and an f or. In the above radius equation: the radius of the circle: From the above radius equation, we can easily say that the circle’s properties, i.e. if > 0 ⇒ the radius of the circle is real, so the circle is also real if < 0 ⇒ the radius of the circle is imaginary (but the center of the circle is real), so the circle is called an imaginary circle. if = 0 ⇒ the radius of the circle is "0", so the circle is called a point circle. From the general equation above, some observations that we can quickly solve the problem are as follows: General equation: x² + y² + 2gx + 2fy + c = 0 ; 1. The general equation for a circle is quadratic2 in both the x and y variables . In the general equation, the coefficient of x² = the coefficient of y² is 3. If we look closely, we can see that there is no term containing 'xy' . We can say that the coefficient of xy is always zero (useful when solving problems) 4 . There are three constant values in the above formula, namely g, f and c. 5. From the radius equation we can say that there will be 3 standard cases depending on the sign of the term inse the square root as shown above. Note: To solve problems related to the circle equation, always keep/keep the coefficients of the x² and y² terms the same, i.e. H. 1 If the coefficient is not 1, try setting it to '1' before solving for the different parameters of circle. For example: if the equation for a given circle is: ax² + ay² + 2gx + 2fy + c = 0 ; and a≠0, then we need to form the coefficients of x² and y² as a unit. If we dive the equation by "a", we can get the unity coefficient of the circle equation given above. x² + y² + 2gx/a + 2fy/a + c/a = 0 ; the center will be given as: (-g/a, -f/a) the radius will be: Steps to find the center and radius of the circle according to the equation ! Follow the steps below to find the center and radius of any circle equation as follows: 1. We know the general circle equation x² + y² + 2gx + 2fy + c = 0; now to find the center and radius of any circle from the general equation , it is important to make the coefficients of the x-squared and y-squared in units. We can then apply the formulas for the center and radius in the equation by substituting in the constant values. 2. Now apply the circle center formula in the equation as (-coefficient of x/2 , -coeff of y/2). 3. Now use the formula to determine the radius of the circle from the general equation, since the radius is equal to.
Steps For Deriving Equation Of A Circle !!
In this section, we will now try to derive the equation for the circle. To derive the equation, we can simply prove that the general equation for each circle is given by: x² + y² + 2gx + 2fy + c = 0 ; now we can write the above equation as: x² + y² + 2gx + 2fy + c = 0 ; also, if we add “g² + f²” to both ses of the above equation, we can write: ( x² + 2gx + g² )+ ( y² + 2fy + f² )= g² + f² – c c ; . ..(with constant term ‘c’ on the right se of equ) Now we have: (x + g)² + (y + f)² = g² + f² – c c … equ (1) we It is already known that there are two fundamental entities in Ath: (a+b)² = a² + 2ab + b² ; (a-b)² = a² – 2ab + b² ; therefore, if we now take the square root of 1) to square the right-hand term in: (x + g)² + (y + f)² = g² + f² – c c … … equ (2 ) Now we know that the standard equ for each circle is given by: (x – h)² + (y – k)² = a² ; …equ(3) Let’s compare equ(2) with the standard equation above, which is H. equ(3) above, we also know that √a * √a = a then we can of course deduce the values given below: h = -g and k = -f, the value of ‘a’ is also given as = a = Now we know from the standard equation (3) that the center of the circle is (h,k) and the radius is ‘a’ So from above we can say that the values of the center and radius of the circle in equation (2) are as follows: The center of the circle = (h, k) = (-g, -f)..(compared to the two equations) the radius is = a = so we have successfully derived and proved the equation x² + y² + 2gx + 2fy + c = 0 ; is the general equation for the center (-g,-f) and radius.
Diameter Form Of A Circle Equation !!
If we have two diameter points, we can also build an equation for a circle. The equation of the circle drawn on the line connecting the two given points (x1 , y1) and (x2 , y2) since the diameter is (x – x1)(x – x2) + (y – y1)( y – y2) is = 0 Note: Given the coordinates of the diameter endpoints of the circle, we can also find the circle equation by finding the center coordinates and the radius coordinates. The center is the center of the diameter, and the radius is half the length of the diameter (where the length can be found using the distance formula).
How To Work Out The Equation Of A Circle ? (Examples Related To Circles Equation Problems !!)
There are many kinds of problems related to the circle equation. Type 1: Find the circle equation given the radius and center: If the center is (2,-3) and the radius is 8, then find the circle equation: We know the standard equation of a. The circle is centered at (h,k) and the radius “a” ” is (x – h)² + (y – k)² = a²; now given here, the center is at (2,-3) and the radius is 8. Put the values in the standard equ above: (x – 2)² + (y – (-3))² = 8² ; when solving the above equation: x² + y² – 4x + 6y – 51 = 0 Type 2: From Given the circle equation to find the center and radius of the circle Let the circle equation be x² + y² + 6x – 4y + = 0 Now let’s find the center and radius of the above equation using the standard equation: (x – h)² + (y – k )² = a² Here we need to convert the given equation to the standard form given above. This can be done using the perfect square technique. Here we need to add and subtract a constant term from both ses of the given equation. The terms added depend on the coefficients of x or y. Remember that you need to add and subtract terms = [(coefficient of x)/2]² + [(coefficient of y)/2]². Now our equation is x² + y² + 6x – 4y + 4 = 0; try converting the above Equ to standard form as (x – h)² + (y – k)² = a² x² + y² + 6x – 4y + 4 = 0; (x² + 6x + 9) + ( y² – 4y + 4 ) = -4 +9 +4 ; .. (add “13” to both ses) For the above equation, we can use the entity as (a+b )² and (a-b)², substitute the values of a and b here, and compare the standard circle equation: (x – (-3))² + (y – 2)² = 3² Combining the above with (x – h) ² + (y – k)² = a² Comparing, we get the circle center is (h, k ) = (-3 ,2) The radius of the circle is ‘a’ = 3 We can even use the general circle equation x² + y² + 2gx + 2fy + c = 0; the center of the circle is (-g , -f) and the radius of the circle is now if we give the equation x² + y² – 6x + 4y – 12 = 0 ; the coefficients of x² and y² are 1, so we The general equation formula can be used: The center of the equation is (-coeff of x/2 , -coeff of y/2) = (3 , -2) The radius of the circle becomes = Now substitute the values of g and f into the general equation form above , we get: Radius = √ ie Radius = √(9+4+12) ∠ = 5 ; therefore, the center is at (3,-2) and the radius is 5 units. Type 3: Given the coordinates of the diameter endpoints, find the equation of the circle. We know that the equation of a circle is drawn on a line connecting two given points (x1, y1) and (x2, y2) with a diameter: (x – x1)(x – x2) + (y – y1 )( y – y2 ) = 0 … equ (1) If the given coordinates are (-1,2) and (4,-3) , these are actually the endpoints of the circle: then the circle equations x1 = -1 , x2 = 4 , y1 = 2 and y2 = -3 Substituting the above values into Eq. (1) a, then: (x – (- 1))(x – 4) + (y – 2)(y – (-3)) = 0 Solving for the above , the equation of the circle is: x² + y² – 3x + y – 10 = 0 Hope to like the above post about equations for circles with different types of problems, and the steps to deduce the general equation of a circle in detail. Stay tuned for more interesting content in this series. report this ad
See some more details on the topic Equation Of A Circle In It’s Standard Form & Some Examples With Steps !! here:
Determine the Equation of a Circle in Standard Form
To determine the center and radius, put this equation into standard form. Standard form is \display (x-h)^2 + (y-k)^2 = r^2, where …
Standard Form of Circle Equation – Expii
The standard form of a circle’s equation is (x-h)² + (y-k)² = r² where (h,k) is the center and r is the radius. To convert an equation to standard form, …
Convert a Circle Equation to the Standard Form – dummies
Learn how to sketch the graph of a circle by using its equation in the standard form. All you need is the circle’s center and radius.
Standard Equation of a Circle With Examples – Turito
Most scientists and mathematicians use the standard form equation of a circle because it gives precise information about the center and …
Related searches to Equation Of A Circle In It’s Standard Form & Some Examples With Steps !!
- Circle distance formula
- how to write an equation of circle in standard form
- circle equation
- polar coordinates
- what is the standard form equation for a circle
- circle wiki
- Polar coordinates
- how to find standard form of the equation of a circle
- The equation of the circle
- directrix
- circle distance formula
- the equation of the circle
- Tangent to the x axis
- Find the radius with endpoints
- find the radius with endpoints
- equation of a circle forms
- how to turn the equation of a circle into standard form
- tangent to the x axis
- Circle equation
- i learned that the equation of a circle is in standard form of its terms are
Information related to the topic Equation Of A Circle In It’s Standard Form & Some Examples With Steps !!
Here are the search results of the thread Equation Of A Circle In It’s Standard Form & Some Examples With Steps !! from Bing. You can read more if you want.
You have just come across an article on the topic Equation Of A Circle In It’s Standard Form & Some Examples With Steps !!. If you found this article useful, please share it. Thank you very much.
