Are you looking for an answer to the topic “How To Find Domain And Range Graphically – Step By Step Guide !!“? We answer all your questions at the website Chambazone.com in category: 40+ Marketing Blog Topics & Ideas. You will find the answer right below.
Keep Reading
Domain and Range of a Function From a Graph
Images related to the topicDomain and Range of a Function From a Graph
In the last article of this series, we saw all the different ways to find the domain and scope of a function. It’s time to learn a smart way to graphically find the domain and scope of any function. To find the domain and range of a graph, you need to learn the basics of graphing any basic mathematical function. In this post, we’ll explore all the steps needed to quickly get the domain and area of a given function using graphs. First, we’ll discuss the standard real functions that are most commonly encountered when learning calculus. Now let’s also look at the standard process you need to follow for any graphics problem.
How to Find Domain And Range Of A Graph ?
Steps to find the domain and domain of a function graphically: Plot f(x) , i.e. in any chart we can have the domain as all the x-coordinate values of the chart (along the x-axis). And the range is all y-coordinate values of the chart (along the y-axis). Finally, we need to carefully include/exclude the endpoints in the interval by looking at the graph (where f(x) is a val function). Now, the above steps will work for any function that involves graphs. If you already have a chart, then go ahead and solve for Domains and Areas (following steps 2 and above). Now is the time to dig into each common feature and see what the scope and domain actually look like.
How To Find Domain And Range Graphically ?
As shown above, the first step is to graph f(x). The key here is to know what the graph of a given real-valued function looks like. Now let’s graph all the commonly used functions and see the domain and range in each specific case. Always remember that to draw random graphs, you must draw your coordinates in the Cartesian plane, which includes four quadrants. In each quadrant, the x-axis and y-axis values are different (negative/positive). To make plotting f(x) easier, you can first plot the x and y coordinates (fewer test points) on the number line (get a rough ea of the shape of the plot.). So if we have point (x,f(x)) then start from point (0,f(0)) , (1,f(1)) and finally find the root of f(x) . Draw the same thing on the diagram. So, without further ado, let’s take a look at the charts of commonly used functions for reference.
Domain And Range Of Constant Function Graph !!
Let’s start with simple functions. Therefore, a constant function is basically a real number that can be expressed as: f(x) = k .. . For all x ∈ R f(x) is called a constant function. This can be represented graphically as follows: Obviously, the graph is a line parallel to the x-axis (the “k” based notation is above/below the x-axis). When k = 0, it coinces with the x-axis. To find the domain of any graph, we start moving from left to right (and look at the beginning and end of the graph along the x-axis). Based on this, we declare the domain of the graph. To find the range of the chart, we start moving from down to up (and look at the start and end of the chart along the y-axis). Based on this, we declare the area of the graph. Since constant functions have no endpoints and tend to infinity. Based on these two conditions, we can easily say that the domain of f(x) is R (all real values on the number line). Furthermore, the range of f(x) is also R (all real values, i.e. -∞ to ∞). on the number line) I hope you understand the process of finding domains and areas from a diagram. Before moving on to the next function, let’s review the definition of function domain and scope. The domain basically refers to all the values of ‘x’ that the function f(x) can accept (the possible input values of ‘x’), the range is defined as the value of the function obtained given the value of ‘x’ is set to ‘ . (all output values of f(x)).
Domain And Range Of An Identity Function Graph !!
Now is the time to learn about the entity function. So an entity function is basically a function that relates any real number to itself, and can be written as: I(x) = x …. For all x ∈ R where I(x) is called the entity function. This can be represented graphically as follows: Obviously, the graph is a straight line through the origin (and inclined 45° from the x-axis). To find the domain of any graph, we start moving from left to right (and look at the beginning and end of the graph along the x-axis). Based on this, we declare the domain of the graph. To find the range of the chart, we start moving from down to up (and look at the start and end of the chart along the y-axis). Based on this, we declare the area of the graph. Since the entity function has no endpoints and tends to infinity. Based on these two conditions, we can easily say that the domain of f(x) is R (all real values on the number line). Furthermore, the range of f(x) is also R (all real values, i.e. -∞ to ∞). on the number line).
Domain And Range Of Modulus Function Graph !!
Now is the time to learn about modulo functions. So the modulo function can basically be written as: then f(x) = |x| = x x ..if x ≥ 0; and f(x) = |x| = -x ..if x ≤ 0; Here f(x) is called the modulo function. Graphically it can be represented as follows: Obviously, the graph is a line through the origin (45° inclined to the x-axis), and then another line through the origin (45° inclined, towards the x-axis) on the other se. (actually a mirror image) To find the domain of any graph, we start moving from left to right (and look at the start and end of the graph along the x-axis). Based on this, we declare the domain of the graph. To find the range of the graph, we start moving from down to up (and look at the beginning and end of the graph along the y-axis). Based on this, we declare the area of the graph. Since the entity function has no endpoints and tends to infinity. Based on these two conditions, we can easily say that the domain of f(x) is R (all real values on the number line). In addition, the range of f(x) includes all positive values of R (all real values, i.e. -∞ to ∞ on the number axis). The value range of the modulo function = the positive values of R, i.e. {x ∈ R : x ≥ 0}.
Domain And Range Of Greatest Integer Function Using Graph !!
For any real number “x”, we use the notation [x] to denote the largest integer function (GIF). Furthermore, we can define the GIF function as the largest integer less than or equal to “x”, which is H. For all x ∈ R, the function f : R → R is defined by f(x) = [x]. For example: [1,76] = 1 , [7.45] = 7 , [-6.87] = -7 , etc. GIF is also known as a step function. Even if we plot the GIF, we can clearly say that the domain of f(x) consists of all R (all real numbers on the number line). A range can be calculated graphically as a set of all integers such as “Z” for example. The range consists of all integer values.
Domain And Range Of Smallest Integer Function Using Graph !!
For any real number “x”, we use the notation [x] to denote the largest integer function (GIF). Furthermore, we can define the GIF function as the smallest integer greater than or equal to “x”, which is H. For all x ∈ R, the function f : R → R is defined by f(x) = [x]. For example: [1,76] = 2 , [7.45] = 8 , [-6.87] = -6 , etc. GIFs are also known as ceiling features. Even if we plot the GIF, we can clearly say that the domain of f(x) consists of all R (all real numbers on the number line). The range can be calculated graphically as a set of all integers, i.e. H. The Z range is the set of all integer values. The
Domain And Range Of Signum Function Using Graph !!
signum function is one of the simplest, with a well-defined constant value of 1 . The function f can be defined as the following predefined conditions: d. H. f(x) = |x|/x x ≠ 0 ; … (x > 0 when f(x) is 1 and x < 0 when -1) and, f(x) = 0 , x = = 0 ; if we graph these conditions, we can clearly see the range and area values. For domains, just start on the left and move to the right. So now f(x) = the domain of R (all values on the number line); and the area of f(x) = {-1 ,0 ,1}.
Domain And Range Of An Exponential Function Using Graph !!
For the exponential function a^x, we can now define it as follows: if a is a positive real number other than 1, the function that associates each x ∈ R with a^x is called an exponential function. It can be given as follows: f(x) = a^x where a > 0 and a ≠ 1 is called an exponential function. Now the domain of f(x) is R and the range of f(x) is determined by all positive values of R except “0”, which is H. Range = (0,∞) because it only reaches positive values. Also, the value of f(x) = a^x is different for different values of “x” and “a”, but the values of domain and range are the same in all cases.
Domain And Range Of Logarithmic Function Using Graph !!
The logarithmic function can be defined as: f(x) = for x > 0 ; also remember that logarithmic and exponential functions are reciprocals of each other. Now let’s draw a graph of the logarithmic function: it is clear from the graph that the domain of f(x) consists of all positive values, which is H. (0,∞), the range of the logarithmic function is R (the set of all real numbers) Note: Always start looking for the domain from left to right, for the range of the function, just go from bottom to top.
Domain And Range Of A Square Root Function Using Graph !!
A square root function is defined as: f(x) = √x and f(x) is only val for positive values of ‘x’ Obviously the domain of this square root function is all positive values of ‘x’. i.e. [0,∞) and the range of f(x) is also [0,∞) . Now let’s look at the graph of the square root function: Note: the graph of the inverse function is also given as: f(x) = 1/x , obviously the domain is all R except ‘0’ and the range is also R – {0}. The
Domain And Range Of A Square Function Using Graph !!
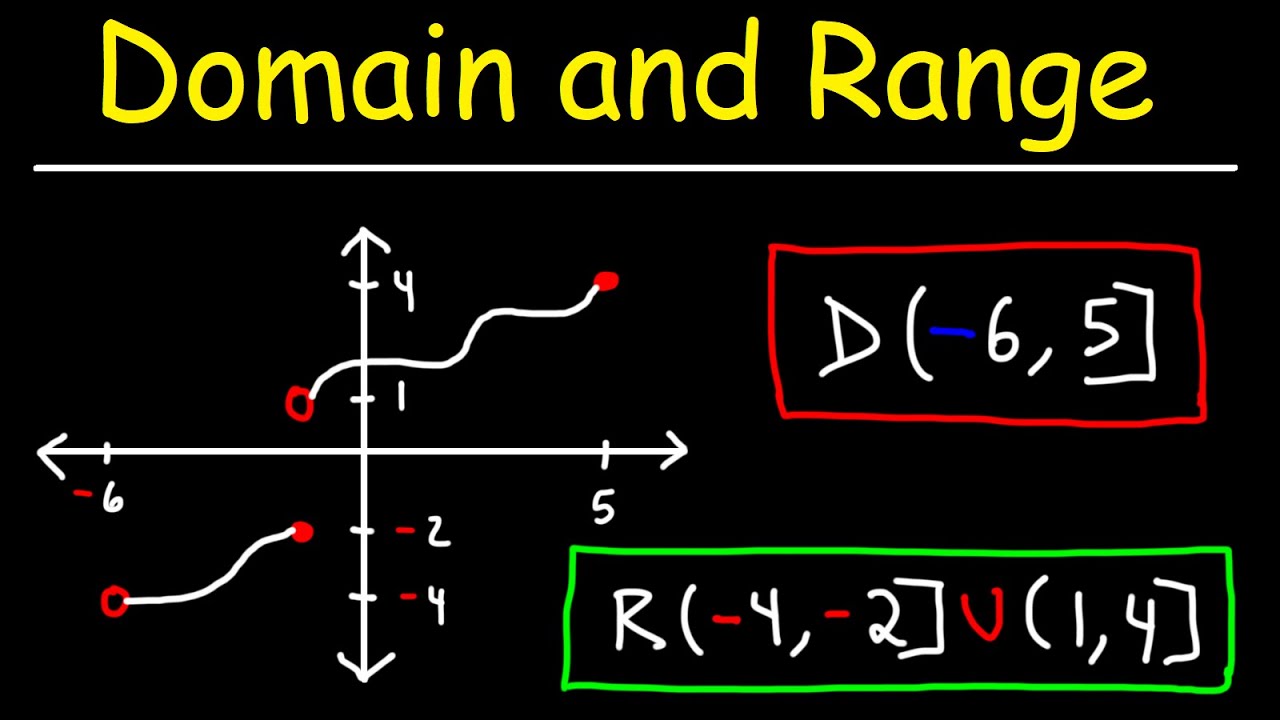
quadratic function will always yield positive values, but it can accept any value in R. A quadratic function is given by: f(x) = x² , which is a quadratic function. Let’s represent the graph of f(x) as follows: The domain of f(x) is a unique R, which is H. (-∞ , ∞) and f(x) are in the range [0,∞) , and the graph of the square function is a parabola. Now let’s try to graphically find the domain and property set next to the default property. Always remember that to find the domain and area of a graph, you need to perform the following steps: 1. To find the domain graphically, start moving from left to right along the x-axis. 2. Now to find the range of the chart, simply move from the downward direction to the upward direction along the y-axis. The above two points will become clear if you solve some examples to find extents and areas graphically. Let’s try to find the domain and area of the graph given below: Of course, if we start moving from left to right, we will first encounter the graph with f(x) at x = -4, and then in the interval x Between = -2 to x = 1, no graph available. Then the graph of f(x) starts from x = 1 again. So from all this we can conclude that the range of f(x) is graphically = [-4 , -2] ∪ [1 , ∞) ; now we need to start moving from the down to the up range. Therefore, we will encounter the graph at x = 0 first, and the graph will continue to infinity. So the range of f(x) is graphically = [0 , ∞).
How To Find Domain And Range Of A Function Graphically ?
When you get a function, the first step is to graph f(x). Then all you have to do in the chart is check the start and end points along the x and y axes to annotate the range and range values. For example: if f(x) = 2x + 5 the x coordinate value of this function (where f(x) is “0”) is unique (-5/2) or. So, knowing this, we can easily The ground is drawn as follows: Now, moving from left to right, the domain in the interval, which is H. (-∞,∞) . For range values, we just move from bottom to top along the y axis, of course the range is the same, i.e. R.
How To Find Domain And Range Of A Quadratic Function Graphically ?
Now this is interesting. First you need to accurately graph a given quadratic function, i.e. a parabola. Also, the opening of the parabola depends on the coefficient of x² in the quadratic equation. Suppose f(x) = ax² + bx + c Now the above equation is a standard quadratic equation, if a > 0 then the graph of f(x) will be: If a < 0 then the graph of f(x) will be: Also remember that the domain of any quadratic equation is always R, which is H. (-∞,∞) which means it can take any value for 'x' and for that we need to pay attention to the range of start and end points of the quadratic equation along the y axis. Now let's try an example to illustrate the concept: Let's try to find the domain and range of the function graphically: f(x) = x² + 5x + 6 Now we need to draw the graph first, let's do this Let's find the root: Using metaphase division, we can write the above function as: f(x) = x² + 5x + 6 † † = †(x+2)(x+3) = 0; the root of the above equation is f(x) = 0; therefore, the roots are given as x = -2 , -3; now plot the same graph: f(x) = x² + 5x + 6 ; the graph looks like this: The domain is clearly R d. H. (-∞,∞) ... (because if we go from left to right, there is no end point along the x-axis) now the range is given as points along the y-axis: as in the graph, along the up direction of the y-axis There are no endpoints for the graph. Now designate the starting point of the graph as a "vertex", where the axis of symmetry == the mpoint of the two roots on the number axis is also f(x) the y-coordinate of the vertex = = set the value of 'x' if equ off f (x ) .. (x is the axis of symmetry) Now the intersection of the graph with the y-axis is, x = 0 f(x) = x² + 5x + 6 ; when setting x = 0 , f(x) = 6 ; now from the figure you can It is clear that f(x) is in the range [y-coordinate of vertex,∞) 2a , -D/4a) , where D = b² – 4ac For the equation f(x) = ax² + bx + c ; apply the formula The formula in : f(x) = x² + 5x + 6 ; a = 1 , b = 5 and c = 6 , also f(x) = (-5/2 , -1/4) of D = 1 vertex , f(x) is in the range [-1/4 , ∞ ) I hope you really enjoyed this post on fast methods for solving graph domains and regions. Let me know in the comments section if you have any questions. Stay tuned for more interesting content in this series. report this ad
How do you find the domain and range of a function graphically?
Another way to identify the domain and range of functions is by using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x-axis. The range is the set of possible output values, which are shown on the y-axis.
How do you solve domain and range step by step?
To find the domain and range, we simply solve the equation y = f(x) to determine the values of the independent variable x and obtain the domain. To calculate the range of the function, we simply express x as x=g(y) and then find the domain of g(y).
How do you find range on a graph?
Another way to identify the domain and range of functions is by using graphs. Because the domain refers to the set of possible input values, the domain of a graph consists of all the input values shown on the x -axis. The range is the set of possible output values, which are shown on the y -axis.
How do you find the domain and range of a function without a graph?
- Step 1 : Put y = f(x)
- Step 2 : Solve the equation y = f(x) for x in terms of y. …
- Step 3 : Find the values of y for which the values of x, obtained from x = g(y) are real and its domain of f.
- Step 4 :
How do you find the domain of a function step by step?
A function with a fraction with a variable in the denominator. To find the domain of this type of function, set the bottom equal to zero and exclude the x value you find when you solve the equation. A function with a variable inside a radical sign.
What is the first step to finding the domain of a function?
To find the domain of a function, just plug the x-values into the quadratic formula to get the y-output. To find the range of a function, first find the x-value and y-value of the vertex using the formula x = -b/2a. Then, plug that answer into the function to find the range.
What is domain and range example?
Example 2:
The domain is the set of x -coordinates, {0,1,2} , and the range is the set of y -coordinates, {7,8,9,10} .
What is a range bar on a graph?
Overview. A range bar chart displays information as a range of data by plotting two Y-values (low and high) per data point. The vertical axis shows the values, and the horizontal axis shows the categories they belong to. So, the range bar chart is a vertical version of the range column chart.
See some more details on the topic How To Find Domain And Range Graphically – Step By Step Guide !! here:
How To Find Domain And Range Graphically – Step By Step …
How To Find Domain And Range Graphically ? As seen above, the first step is to plot the graph of f(x) . Here the foremost point is to know …
Domain and Range – Algebra and Trigonometry – BC Open …
Find the domain of a function defined by an equation. Graph piecewise-defined functions. If you’re in the mood for a scary movie, you may want to check out one …
Determining the Domain and Range for Linear Functions
Given a real-world situation that can be modeled by a linear function or a graph of a linear function, the student will determine and represent the …
How to Find Domain and Range of a Function? – Effortless Math
The domain and range of any function can be found algebraically or graphically. Step by Step gue to finding domain and range.
Related searches to How To Find Domain And Range Graphically – Step By Step Guide !!
Information related to the topic How To Find Domain And Range Graphically – Step By Step Guide !!
Here are the search results of the thread How To Find Domain And Range Graphically – Step By Step Guide !! from Bing. You can read more if you want.
You have just come across an article on the topic How To Find Domain And Range Graphically – Step By Step Guide !!. If you found this article useful, please share it. Thank you very much.
